この記事の目次
なぜ小論文でグラフ問題が出題されるのか
突然ですが、なぜSFCの小論文ではグラフの読み取り問題が出題されるのでしょうか。近年、STEAM教育や情報活用能力に注目が集まっていることが背景にあるといえるでしょう。STEAM能力とは
S cence
T echnoloy
E nginneering
A rt
M athematics
の5技能で、これからより一層情報化が進んでいく社会で求められる能力とされ、理数系能力が多くを占めています。さらに近年共通テストの傾向などからも、グラフの読み取りやデータなど、情報活用能力への注目が高まっていることもわかるでしょう。また、SFCでは特に総合政策学部の小論文で、グラフの読み取りが要求される問題が特徴的となっています。また、SFCではデータサイエンス科目(数学や統計、データに関する科目)が必修になっており、学生にデータサイエンスの力が求められていると言えます。これらのことからもSFC小論文において、また大学入試全体においてグラフの読み取り問題の対策が必須であると言えるでしょう。
グラフを読む際のポイント
- 最大値、最小値
データの規模の解釈に役立ちます - 平均、分散、中央値
データの分布の理解に役立ちます - サンプルサイズ(n数)、データの出展
データの意味を解釈する上で前提となるので必ず確認しましょう。 - 増えたのか、減ったのか
時系列の時、マイナスからプラス、プラスからマイナスなどの変化があるところは何かしらの出来事が発生している可能性が高いです。 - 特異点、外れ値
これに関しても同様に、その点における重要な特徴を表している場合があります。
グラフの種類と読み取り方
棒グラフ
データの大きさの比較に向く一方で、連続性のあるデータを表現するのには向かないため、単純な数字の比較の際に使われます。

折れ線グラフ
時系列などの連続性のあるデータの表現に向いています。増減が変化するところに注目すると小論文に活かしやすくなるでしょう。
円グラフ
構成要素の割合を表すのに向いているものの、比較には向かないグラフとなっています。
積み上げ棒グラフ
複数要素を積み上げた棒グラフで、割合の表現も可能です。円グラフよりも割合の比較に長けている点で優秀なグラフです。

散布図
二つのデータの関係性を表すのに向いています。相関やばらつきの大きさに注目しましょう。
- 右上がり→xが増えるとyも増える
- 右下がり→x が増えるとyが減る
- 分散大→xとyはあまり関係していない
- 分散小→xとyは強く関係している

バブルチャート
散布図に縁の大きさを追加した表現方法になっていて、3つのデータの関係性を表すのに向いています。散布図と同様に読み取ることができますが、円の大きさにも注目するようにしましょう。

ヒストグラム
データの分布がわかりやすいです。次に紹介する箱ひげ図に比べると細かい分布がわかりやすくなっています。
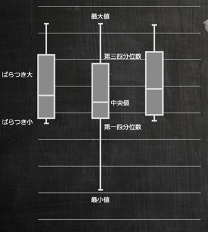
箱ひげ図
最小値、第一四分位数(下から4分の1の値)、中央値(真ん中の値)、第三四分位数(上から4分の1の値)、最大値を表しています。ヒストグラムより分布の表現は大雑把ですが、図のように並べて比較することができる点で優れています。
グラフを読み取る際の注意点
目盛に注意
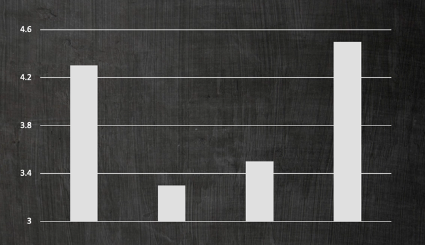
軸が途中から始まっていたり途中でカットされたりしていると、必要以上に差を大きく解釈してしまったり、小さく解釈してしまったりする可能性がある
間隔に注意
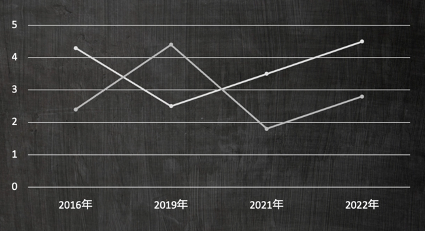
目盛の間隔が変わるとグラフの形も変わってしまう

分類の仕方を変えたりサンプルの大きさを変えたりすると分布を操作できる
グラフ問題の対策方法
グラフの読み取り問題はとにかくたくさんのグラフを読むことが大切です。SFCの問題が難しいと言う人は共通テストの過去問や予想問題集などから取り組んでみると良いでしょう。私は理系でしたが、地理や数学は特にグラフ問題が多い印象でした。先述した通り共通テストでもグラフの読み取り問題が増加傾向にあります。SFCよりは比較的解きやすい共通テストから上記のことを意識して対策を積むと良いでしょう。また、SFCの過去問を解くことも非常に有効です。特に総合政策学部2020年や総合政策学部2019年、総合政策学部2016年はグラフの読み取りを中心に問題が構成されている部分があります。グラフ問題に苦手知識がある人は総合政策学部の過去問を優先して対策を積んでいくと良いでしょう。








-320x180.png)








